Solving linear equation systems in Linux
Maxima is an open source system for the manipulation of symbolic and numerical expressions.
di Lorenzo Clementi |
Commenti |
Tempo di lettura: 1 - 2 min
A few days ago, while working at an exercise paper for the lecture Information Theory, Gionni, Micheal and I were confronted with the need to solve the following equation system:
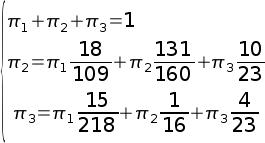
After a fruitless Google search, I recalled that some time in the past I had heard about a tool called maxima.
And, I found out, Maxima is indeed a very powerful scientific calculator.
The following code allowed us to solve the equation system:
linsolve ([x+y+z=1,
y=(18/109)*x+(131/160)*y+(10/23)*z,
z=(15/218)*x+(1/16)*y+(4/23)*z],
[x, y, z]);
producing the following, exact result:
x = 98318/250043
y = 133440/250043
z = 18285/250043
Further, it is possible to get an approximated result by using the function float:
float(linsolve ([x+y+z=1,
y=(18/109)*x+(131/160)*y+(10/23)*z,
z=(15/218)*x+(1/16)*y+(4/23)*z],
[x, y, z]));
and here is the corresponding output:
x = 0.39320436884856
y = 0.53366820906804
z = 0.073127422083402
This page provides several links to Maxima Documentation. I found A Maxima Guide for Calculus Students very helpful!
Update (11/05/2007)
The previous equation system is used to solve the exercise 1.2 of the exercise paper attached to this post.
Update (15/06/2007)
The following code is used to define a function:
define('(log2(x)), (log(x) / log(2)) );
Questo post ha un allegato: scaricalo qui.


















